

The area would seem to a 3D being like a small planet that could be walked on in all 3D direction. The 3 sphere represent 3D slices of an observable 3D space. Hyper plan is a project that will foucus on the combination of multiple spacial dimensions and how they would live together.Īs you can see this is a 4D rock, sperated in approximately 3 cross-sections (and befor you say it in the comments, I now that a 4D object has infinite 3D slices but it would be physically impossible to represent 4D if not by simplifying it. Prasolov & VM Tikhomirov (1997,2001) Geometry, page 22, volume 200 in Translations of Mathematical Monographs, American Mathematical Society, Providence ISBN:0-8218-2038-9. Heinrich Guggenheimer (1977) Applicable Geometry, page 7, Krieger, Huntington ISBN:0-88275-368-1.Curtis (1968) Linear Algebra, page 62, Allyn & Bacon, Boston. The Foundations of Topological Analysis: A Straightforward Introduction: Book 2 Topological Ideas. ↑ Polytopes, Rings and K-Theory by Bruns-Gubeladze.↑ Beutelspacher, Albrecht Rosenbaum, Ute (1998), Projective Geometry: From Foundations to Applications, Cambridge University Press, p. 10, ISBN 9780521483643.↑ "Excerpt from Convex Analysis, by R.T.The theory of polyhedra and the dimension of the faces are analyzed by looking at these intersections involving hyperplanes. The intersection of P and H is defined to be a "face" of the polyhedron. In Cartesian coordinates, such a hyperplane can be described with a single linear equation of the following form (where at least one of the \displaystyle. Some of these specializations are described here.Īn affine hyperplane is an affine subspace of codimension 1 in an affine space. Several specific types of hyperplanes are defined with properties that are well suited for particular purposes. A hyperplane in a Euclidean space separates that space into two half spaces, and defines a reflection that fixes the hyperplane and interchanges those two half spaces. If V is a vector space, one distinguishes "vector hyperplanes" (which are linear subspaces, and therefore must pass through the origin) and "affine hyperplanes" (which need not pass through the origin they can be obtained by translation of a vector hyperplane). The space V may be a Euclidean space or more generally an affine space, or a vector space or a projective space, and the notion of hyperplane varies correspondingly since the definition of subspace differs in these settings in all cases however, any hyperplane can be given in coordinates as the solution of a single (due to the "codimension 1" constraint) algebraic equation of degree 1. In geometry, a hyperplane of an n-dimensional space V is a subspace of dimension n − 1, or equivalently, of codimension 1 in V.
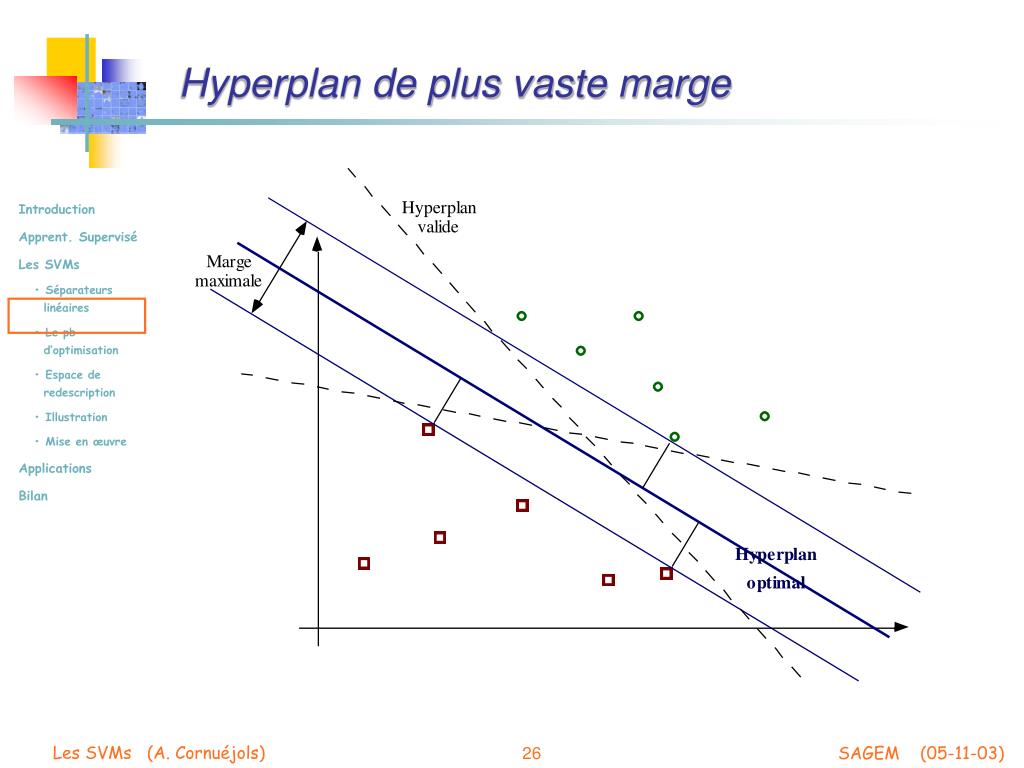
Therefore, a necessary and sufficient condition for S to be a hyperplane in X is for S to have codimension one in X. The difference in dimension between a subspace S and its ambient space X is known as the codimension of S with respect to X. While a hyperplane of an n-dimensional projective space does not have this property. For instance, a hyperplane of an n-dimensional affine space is a flat subset with dimension n − 1 and it separates the space into two half spaces. In different settings, hyperplanes may have different properties. This notion can be used in any general space in which the concept of the dimension of a subspace is defined. For example, if a space is 3-dimensional then its hyperplanes are the 2-dimensional planes, while if the space is 2-dimensional, its hyperplanes are the 1-dimensional lines. In geometry, a hyperplane is a subspace whose dimension is one less than that of its ambient space. A plane is a hyperplane of dimension 2, when embedded in a space of dimension 3. Two intersecting planes in three-dimensional space.


 0 kommentar(er)
0 kommentar(er)
